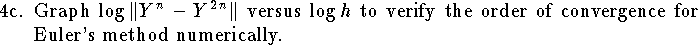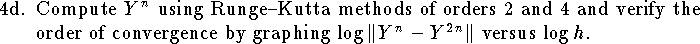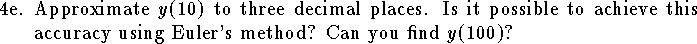Programming Assignment Four
Your work should be presented in the form of a typed report
using clear and properly punctuated English.
Where appropriate include full program listings and output.
If you choose to work in a group of two, please turn in
independently prepared reports.
![\hangindent\parindent
\item{4a.}
The Lorenz system is a three dimensional ordinary differential
equation of the form
$$
{dy\over dt}=f(y)
$$
with a given initial condition $y(0)=a$
where $y(t)$ is a vector in ${\bf R}^3$ and
$$
f(y)=\left[
\matrix{-10 y_1+10 y_2\cr
28 y_1-y_2-y_1 y_3\cr
y_1 y_2-(8/3) y_3\cr}
\right].
$$
Let $Y^n$ be an approximation of $y(1)$ obtained
using a step size of $h=1/n$.
Define the error
$$E_n=\|Y^n-y(1)\|=\left\{\sum_{i=1}^3
\big(Y^n_i-y_i(1)\big)^2
\right\}^{1/2}.
$$
Show that if $E_n\le K h^k$ then
$$
\|Y^n-Y^{2n}\|\le K \Big\{1+{1\over 2^k}\Big\} h^k.
$$](a4-1.gif)
![\item{4b.}
Write a program to approximate solutions
of the Lorenz system using Euler's forward difference
method
and the initial condition
$$
a=\left[\matrix {2\cr3\cr15}\right].
$$
Compute $Y^n$ for $n=64,128,256,512,\ldots,65536$.](a4-2.gif)
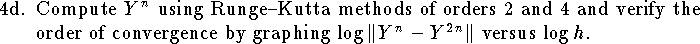
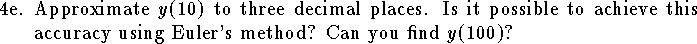
Last updated: Tue Nov 12 14:46:38 PST 2002
![\hangindent\parindent
\item{4a.}
The Lorenz system is a three dimensional ordinary differential
equation of the form
$$
{dy\over dt}=f(y)
$$
with a given initial condition $y(0)=a$
where $y(t)$ is a vector in ${\bf R}^3$ and
$$
f(y)=\left[
\matrix{-10 y_1+10 y_2\cr
28 y_1-y_2-y_1 y_3\cr
y_1 y_2-(8/3) y_3\cr}
\right].
$$
Let $Y^n$ be an approximation of $y(1)$ obtained
using a step size of $h=1/n$.
Define the error
$$E_n=\|Y^n-y(1)\|=\left\{\sum_{i=1}^3
\big(Y^n_i-y_i(1)\big)^2
\right\}^{1/2}.
$$
Show that if $E_n\le K h^k$ then
$$
\|Y^n-Y^{2n}\|\le K \Big\{1+{1\over 2^k}\Big\} h^k.
$$](a4-1.gif)
![\hangindent\parindent
\item{4a.}
The Lorenz system is a three dimensional ordinary differential
equation of the form
$$
{dy\over dt}=f(y)
$$
with a given initial condition $y(0)=a$
where $y(t)$ is a vector in ${\bf R}^3$ and
$$
f(y)=\left[
\matrix{-10 y_1+10 y_2\cr
28 y_1-y_2-y_1 y_3\cr
y_1 y_2-(8/3) y_3\cr}
\right].
$$
Let $Y^n$ be an approximation of $y(1)$ obtained
using a step size of $h=1/n$.
Define the error
$$E_n=\|Y^n-y(1)\|=\left\{\sum_{i=1}^3
\big(Y^n_i-y_i(1)\big)^2
\right\}^{1/2}.
$$
Show that if $E_n\le K h^k$ then
$$
\|Y^n-Y^{2n}\|\le K \Big\{1+{1\over 2^k}\Big\} h^k.
$$](a4-1.gif)
![\item{4b.}
Write a program to approximate solutions
of the Lorenz system using Euler's forward difference
method
and the initial condition
$$
a=\left[\matrix {2\cr3\cr15}\right].
$$
Compute $Y^n$ for $n=64,128,256,512,\ldots,65536$.](a4-2.gif)