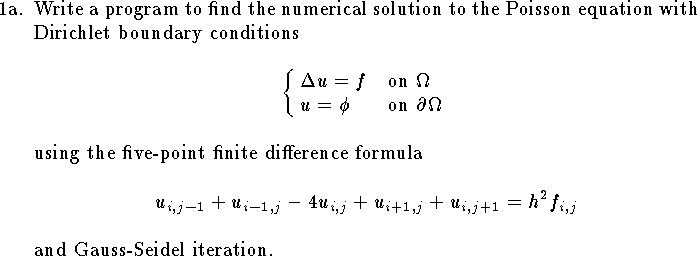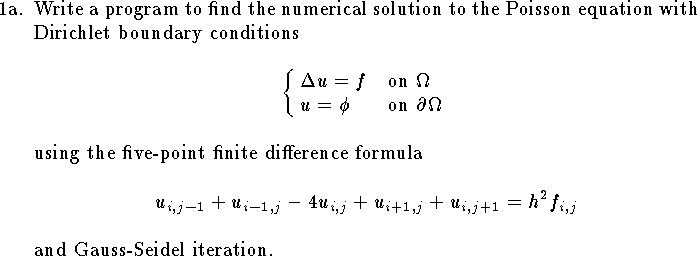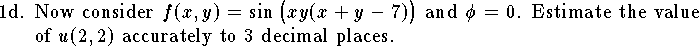Programming Assignment One

Your work should be presented in the form of a typed report using clear and properly punctuated English. Where appropriate include full program listings and output. If you choose to work in a group of two, please turn in independently prepared reports.

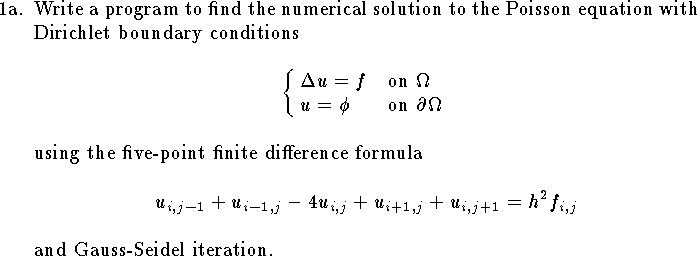
$\hangindent\parindent \item{1a.} Write a program to find the numerical solution to the Poisson equation with Dirichlet boundary conditions $$ \cases{ \Delta u=f&on $\Omega$\cr u=\phi& on $\partial\Omega$ } $$ using the five-point finite difference formula $$ u_{i,j-1}+u_{i-1,j}-4u_{i,j}+u_{i+1,j}+u_{i,j+1}= h^2 f_{i,j} $$ and Gauss-Seidel iteration.$

$\item{1b.} Note that if $\Delta\phi=f$ then $u=\phi$ is the exact solution on all of $\Omega$. Using this observation, test your program for $f=0$ and $\phi(x,y)=x-2y$ on the domain $\Omega$ whose boundary $\partial \Omega$ consists of the triangle whose vertices are $(0,0)$, $(7,0)$ and $(0,7)$. Try values of $h$ equal to $2$, $1$, $1/2$, $1/4$ and $1/8$.$

$\item{1c.} How do the approximations of $u$ found in the previous step depend on grid spacing? Explain your results in terms of the order of accuracy in the five-point formula and the specific form of $\phi$ used.$

$\item{1d.} Now consider $f(x,y)=\sin\big(xy(x+y-7)\big)$ and $\phi=0$. Estimate the value of $u(2,2)$ accurately to 3 decimal places.$

$\item{1e.} Modify your program to use successive over-relaxation. Determine the optimum value of the relaxation parameter $\omega$ for a grid spacing of size $h=1/8$. Does the optimal value of $\omega$ depend on $f$ or $\phi$? Does it depend on $h$?$

Last Updated: Tue Feb 25 16:26:03 PST 2003