Programming Assignment Two
Your work should be presented in the form of a typed report using clear and
properly punctuated English. Where appropriate include full program listings
and output. If you choose to work in a group of two, please turn in
independently prepared reports.
![\def\R{{\bf R}}
\def\Z{{\bf Z}}
\hangindent\parindent
\item{1a.} Consider the viscous Burgers equation
$$u_t-u_{xx}+2u u_x=0\quad
\hbox{where $x\in[0,2\pi]$ and $t\ge 0$}$$
with initial condition
$u(x,0)=u_0(x)$ and periodic boundary
conditions $u(0,t)=u(2\pi,t)$.
Derive the semi-discrete spectral method
$$
{d \hat u_k\over dt} + k^2 \hat u_k +
\sum_{m=-\min(n,n-k)}^{\min(n,n+k)} ik \hat u_{k-m} \hat u_m = 0
$$
by making the the approximation
$$u(x,t)\approx\sum_{k=-n}^n \hat u_k(t) e^{ikx}.$$](a2-1.gif)

![\item{1c.}
Let ${\cal F}$ denote the Fourier transform on
the interval $[0,2\pi]$.
The convolution theorem may be used to obtain that
$$ \eqalign{
\sum_{m=-\min(n,n-k)}^{\min(n,n+k)} ik \hat u_{k-m} \hat u_m
&=ik {\cal F}\big\{({\cal F}^{-1} \hat u )^2\big\}_k.
}$$
Compare the number operations needed to evaluate
the sum directly with the
number of operations needed to evaluate it by
means of a fast Fourier transform.
Note that the Fourier transform method obtains the
sum for all values of $k$ simultaneously.
How does the total computational cost of each method
depend on $n$?](a2-3.gif)
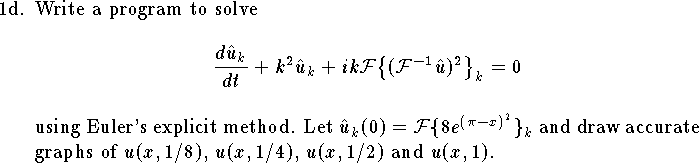
![\item{1e.}
Consider the semi-discrete central difference method
$$
{d u_j\over dt}
-{1\over (\Delta x)^2}(u_{j-1}-2u_j+u_{j+1})
+{1\over \Delta x}u_j(u_{j+1}-u_{j-1})=0.
$$
By taking $u_{n}=u_{0}$ and $u_{-1}=u_{n-1}$
this method may also be used to compute periodic
solutions.
Write a program using Euler's explicit method
to solve these equations.
Let $u(x,0)=8e^{(\pi-x)^2}$ on $[0,2\pi]$
and compare the graphs of
$u(x,1/8)$, $u(x,1/4)$, $u(x,1/2)$
and $u(x,1)$ with those found in
the previous step.](a2-5.gif)
![\item{1f.}
[Extra Credit]
Replace Euler's explicit method for the time
integration by the explicit Runga-Kutta method of order four
given by
$$ \eqalign{
K_0&=\Delta t\, F(u^m)\cr
K_1&=\Delta t\, F(u^m+K_0/2)\cr
K_2&=\Delta t\, F(u^m+K_1/2)\cr
K_3&=\Delta t\, F(u^m+K_2)\cr
u^{m+1}&=u^m+{1\over 6}(K_0+2K_1+2K_2+K_3)}
$$
and find $u(3\pi/2,1/8)$ accurately to 3 decimal places.](a2-6.gif)
Last Updated:
Thu Apr 10 04:21:09 PDT 2003
![\def\R{{\bf R}}
\def\Z{{\bf Z}}
\hangindent\parindent
\item{1a.} Consider the viscous Burgers equation
$$u_t-u_{xx}+2u u_x=0\quad
\hbox{where $x\in[0,2\pi]$ and $t\ge 0$}$$
with initial condition
$u(x,0)=u_0(x)$ and periodic boundary
conditions $u(0,t)=u(2\pi,t)$.
Derive the semi-discrete spectral method
$$
{d \hat u_k\over dt} + k^2 \hat u_k +
\sum_{m=-\min(n,n-k)}^{\min(n,n+k)} ik \hat u_{k-m} \hat u_m = 0
$$
by making the the approximation
$$u(x,t)\approx\sum_{k=-n}^n \hat u_k(t) e^{ikx}.$$](a2-1.gif)
![\def\R{{\bf R}}
\def\Z{{\bf Z}}
\hangindent\parindent
\item{1a.} Consider the viscous Burgers equation
$$u_t-u_{xx}+2u u_x=0\quad
\hbox{where $x\in[0,2\pi]$ and $t\ge 0$}$$
with initial condition
$u(x,0)=u_0(x)$ and periodic boundary
conditions $u(0,t)=u(2\pi,t)$.
Derive the semi-discrete spectral method
$$
{d \hat u_k\over dt} + k^2 \hat u_k +
\sum_{m=-\min(n,n-k)}^{\min(n,n+k)} ik \hat u_{k-m} \hat u_m = 0
$$
by making the the approximation
$$u(x,t)\approx\sum_{k=-n}^n \hat u_k(t) e^{ikx}.$$](a2-1.gif)

![\item{1c.}
Let ${\cal F}$ denote the Fourier transform on
the interval $[0,2\pi]$.
The convolution theorem may be used to obtain that
$$ \eqalign{
\sum_{m=-\min(n,n-k)}^{\min(n,n+k)} ik \hat u_{k-m} \hat u_m
&=ik {\cal F}\big\{({\cal F}^{-1} \hat u )^2\big\}_k.
}$$
Compare the number operations needed to evaluate
the sum directly with the
number of operations needed to evaluate it by
means of a fast Fourier transform.
Note that the Fourier transform method obtains the
sum for all values of $k$ simultaneously.
How does the total computational cost of each method
depend on $n$?](a2-3.gif)
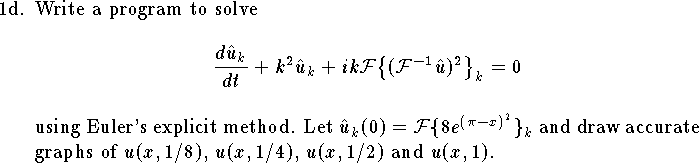
![\item{1e.}
Consider the semi-discrete central difference method
$$
{d u_j\over dt}
-{1\over (\Delta x)^2}(u_{j-1}-2u_j+u_{j+1})
+{1\over \Delta x}u_j(u_{j+1}-u_{j-1})=0.
$$
By taking $u_{n}=u_{0}$ and $u_{-1}=u_{n-1}$
this method may also be used to compute periodic
solutions.
Write a program using Euler's explicit method
to solve these equations.
Let $u(x,0)=8e^{(\pi-x)^2}$ on $[0,2\pi]$
and compare the graphs of
$u(x,1/8)$, $u(x,1/4)$, $u(x,1/2)$
and $u(x,1)$ with those found in
the previous step.](a2-5.gif)
![\item{1f.}
[Extra Credit]
Replace Euler's explicit method for the time
integration by the explicit Runga-Kutta method of order four
given by
$$ \eqalign{
K_0&=\Delta t\, F(u^m)\cr
K_1&=\Delta t\, F(u^m+K_0/2)\cr
K_2&=\Delta t\, F(u^m+K_1/2)\cr
K_3&=\Delta t\, F(u^m+K_2)\cr
u^{m+1}&=u^m+{1\over 6}(K_0+2K_1+2K_2+K_3)}
$$
and find $u(3\pi/2,1/8)$ accurately to 3 decimal places.](a2-6.gif)