M119 Review Answers
-
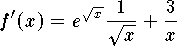 .
.
-
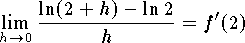 where
where  . Since
. Since 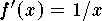 then the answer is
then the answer is
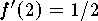 .
.
-
 .
.
- There is a relative maximum at
 and a relative minimum at
and a relative minimum at 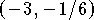 .
.
- Let
 be the area of the poster and
be the area of the poster and  be the
area of the printed matter.
Then
be the
area of the printed matter.
Then 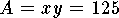 and
and 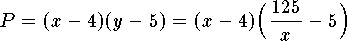 .
It follows that
.
It follows that  when
when 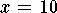 .
This is a maximum because
.
This is a maximum because 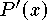 is positive for
is positive for 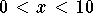 and negative for
and negative for 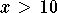 .
The dimensions of the poster should be
.
The dimensions of the poster should be 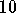 inches
wide by
inches
wide by 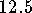 inches high.
inches high.
-
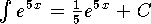 .
Setting
.
Setting  yeilds
that
yeilds
that  .
It follows that
.
It follows that  .
.
- Set
 so that
so that 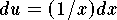 .
The integral becomes
.
The integral becomes 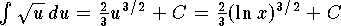 .
.
-
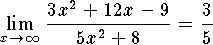 .
.
- Use implicit differentiation. Hence
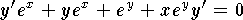 so
that
so
that 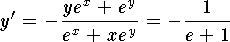 .
.
- Solve for
 in
in 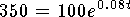 to get
to get
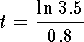 .
.
-
 and
and 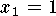 ,
, 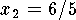 ,
, 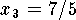 ,
,
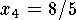 ,
, 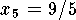 .
Therefore the Riemann sum is
.
Therefore the Riemann sum is
 .
.
-
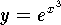 ,
, 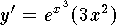 ,
,
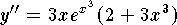 .
If follows
.
If follows 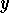 is increasing on
is increasing on 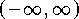 ,
concave up on
,
concave up on 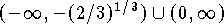 ,
and concave down on
,
and concave down on 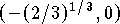 .
.
-
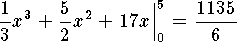 .
.
- Using properties of logarithms
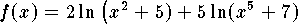 .
Thus
.
Thus 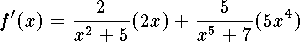 and
and 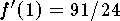 .
.
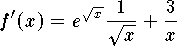 .
.
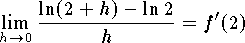 where
where  . Since
. Since 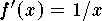 then the answer is
then the answer is
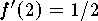 .
.
 .
.
 and a relative minimum at
and a relative minimum at 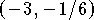 .
.
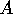 be the area of the poster and
be the area of the poster and 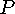 be the
area of the printed matter.
Then
be the
area of the printed matter.
Then 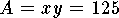 and
and 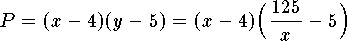 .
It follows that
.
It follows that  when
when 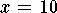 .
This is a maximum because
.
This is a maximum because 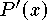 is positive for
is positive for 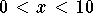 and negative for
and negative for 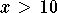 .
The dimensions of the poster should be
.
The dimensions of the poster should be 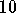 inches
wide by
inches
wide by 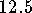 inches high.
inches high.
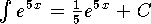 .
Setting
.
Setting  yeilds
that
yeilds
that  .
It follows that
.
It follows that  .
.
 so that
so that 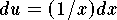 .
The integral becomes
.
The integral becomes 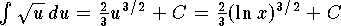 .
.
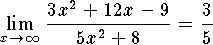 .
.
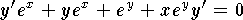 so
that
so
that 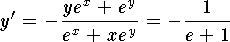 .
.
 in
in 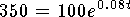 to get
to get
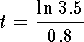 .
.
 and
and 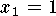 ,
, 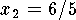 ,
, 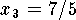 ,
,
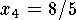 ,
, 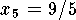 .
Therefore the Riemann sum is
.
Therefore the Riemann sum is
 .
.
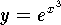 ,
, 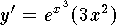 ,
,
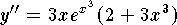 .
If follows
.
If follows 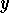 is increasing on
is increasing on 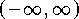 ,
concave up on
,
concave up on 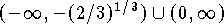 ,
and concave down on
,
and concave down on 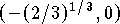 .
.
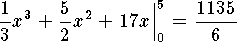 .
.
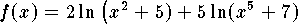 .
Thus
.
Thus 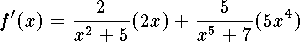 and
and 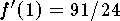 .
.