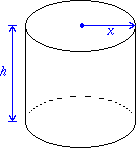
Soup Can Solution
A large soup can is to be designed so that the can will hold
36 cubic inches of soup.
 Find the values of
Find the values of 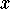 and
and 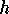 for which the amount of metal
needed is as small as possible.
What is the value of
for which the amount of metal
needed is as small as possible.
What is the value of 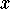 ?
What is the value of
?
What is the value of 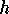 ?
?
The soup can consists of metal for a top, a bottom, and the
piece that wraps around for the side. The total amount of
metal used is
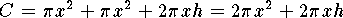 where both
where both 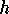 and
and 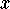 must be positive
numbers.
Since the total volume of the soup can must be 36 cubic inches,
it follows that
must be positive
numbers.
Since the total volume of the soup can must be 36 cubic inches,
it follows that
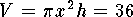 from which one may solve for
from which one may solve for 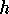 to get
to get
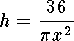 .
Substitute into the expression for the total amount of metal.
.
Substitute into the expression for the total amount of metal.
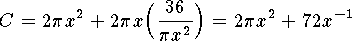 Differentiate.
Differentiate.
 Set the derivative equal to zero and solve for
Set the derivative equal to zero and solve for 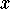 .
.

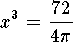
Hence
 inches
and
inches
and
 inches
This is indeed the dimensions for minimum amount of metal
since
inches
This is indeed the dimensions for minimum amount of metal
since 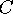 becomes infinite as
becomes infinite as 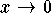 and also as
and also as 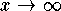 .
.
 Find the values of
Find the values of 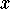 and
and 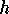 for which the amount of metal
needed is as small as possible.
What is the value of
for which the amount of metal
needed is as small as possible.
What is the value of 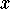 ?
What is the value of
?
What is the value of 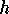 ?
?
 Find the values of
Find the values of 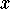 and
and 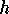 for which the amount of metal
needed is as small as possible.
What is the value of
for which the amount of metal
needed is as small as possible.
What is the value of 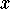 ?
What is the value of
?
What is the value of 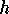 ?
?
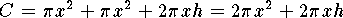
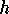 and
and 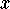 must be positive
numbers.
Since the total volume of the soup can must be 36 cubic inches,
it follows that
must be positive
numbers.
Since the total volume of the soup can must be 36 cubic inches,
it follows that
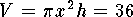
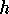 to get
to get
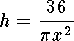 .
.
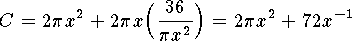

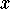 .
.

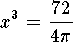
 inches
inches
 inches
inches
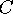 becomes infinite as
becomes infinite as 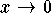 and also as
and also as 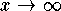 .
.