The Euler-Masheroni Constant

Let $H_n$ be the sum of the first $n$ terms of the harmonic series $$ H_n=\sum_{k=1}^n {1\over k} $$

function H(n)
    r=0
    for k=1:n
        r=r+1/k
    end
    return r
end

H (generic function with 1 method)

H(10)

2.9289682539682538

A simple Calculus argument shows that $$ \ln(1+n)\le H_n\le 1+\ln n $$

The upper bound may be obtained as

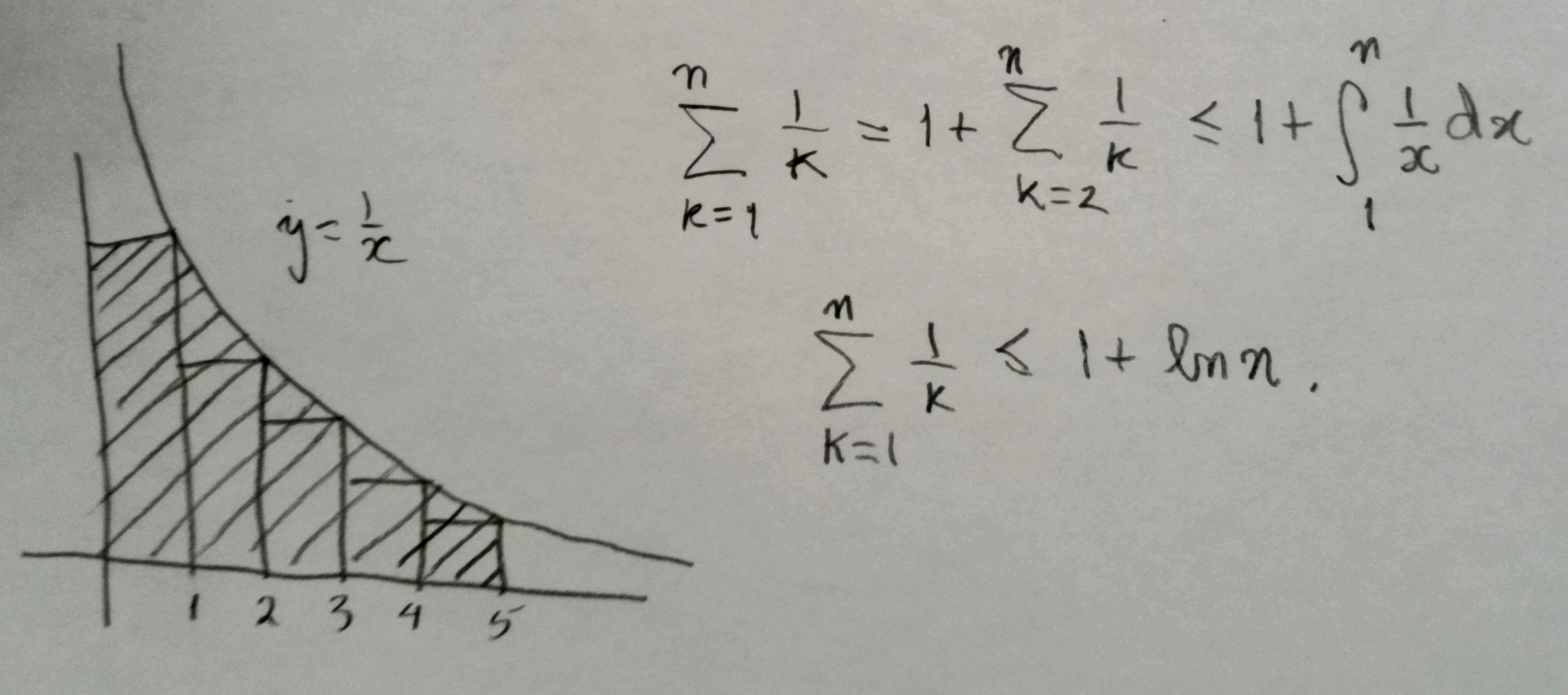
while the lower as

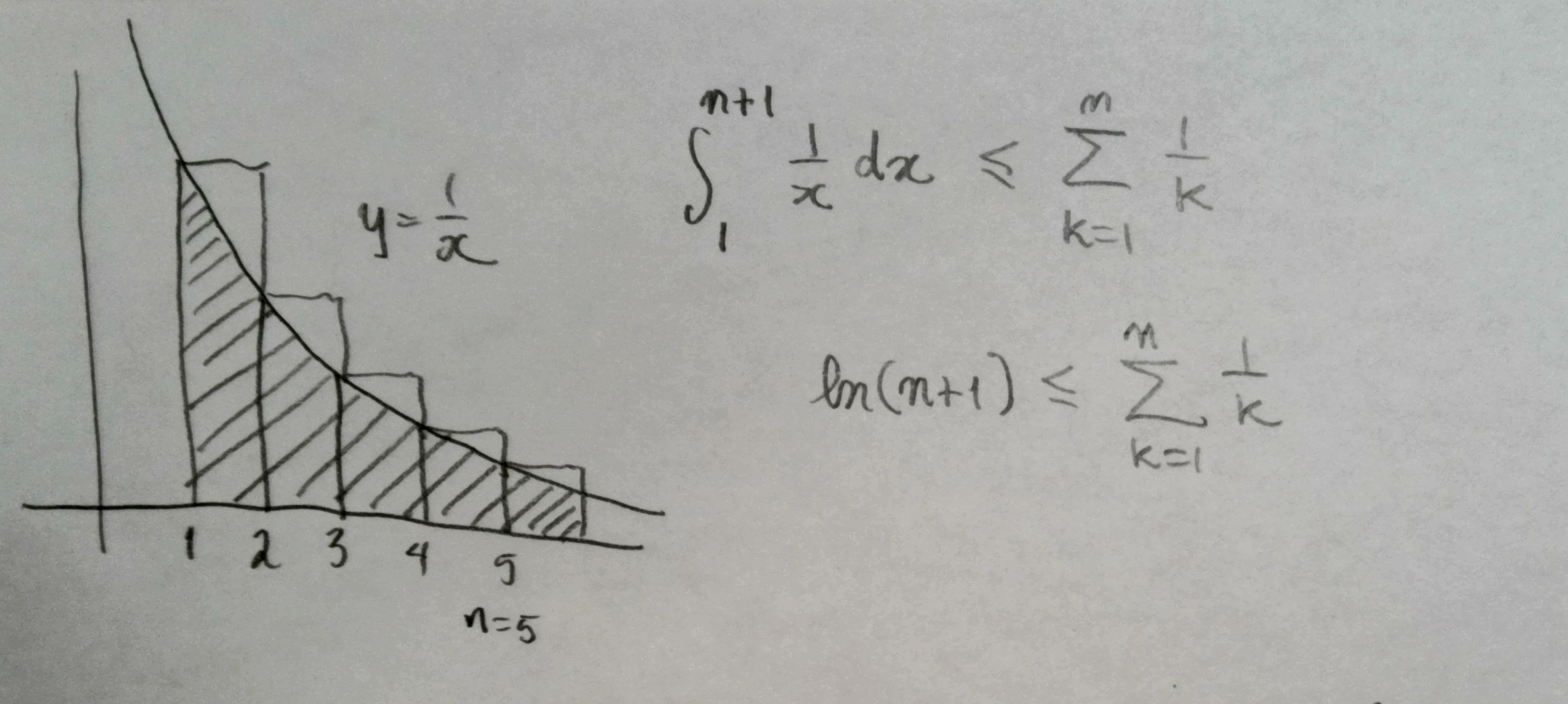
The Euler-Mascheroni constant $\gamma$ is given by the limit $$ \gamma=\lim_{n\to\infty}(H-n-\ln n) \approx 0.5772 $$

for j=1:20
    n=2^j
    println("n=$n, gamma=",H(n)-log(n))
end

n=2, gamma=0.8068528194400547
n=4, gamma=0.6970389722134425
n=8, gamma=0.6384156011773068
n=16, gamma=0.6081402709892125
n=32, gamma=0.5927592926367935
n=64, gamma=0.585007820346096
n=128, gamma=0.5811168286695567
n=256, gamma=0.5791675183377185
n=512, gamma=0.5781919095102124
n=1024, gamma=0.5777038666786787
n=2048, gamma=0.5774597856583172
n=4096, gamma=0.5773377302469473
n=8192, gamma=0.577276698815977
n=16384, gamma=0.5772461821692296
n=32768, gamma=0.5772309236129889
n=65536, gamma=0.57722329427666
n=131072, gamma=0.5772194795937917
n=262144, gamma=0.5772175722491291
n=524288, gamma=0.5772166185756209
n=1048576, gamma=0.5772161417378925