Math/CS 466/666

466/666 NUMERICAL METHODS I (3+0) 3 credits

Instructor  Course Section                     Time              Room
------------------------------------------------------------------------
Eric Olson  Math 466/666 Numerical Methods I   MWF 9-9:50am      DMS106

            CS 466/666 Numerical Methods I     M   2:30-3:45pm   DMS106
                                                W  2:30-3:45pm   SEM340

Course Information

Instructor:

Eric Olson

email:

ejolson at unr dot edu

Office:

Monday, Wednesday and Friday 10am DMS 238 and by appointment.

Homepage:

http://fractal.math.unr.edu/~ejolson/466/

Assistant:

Jordan Blocher

Jordan's email:

jordanblocher at gmail dot com

Required Texts:

Justin Solomon, Numerical Algorithms: Methods for Computer Vision, Machine Learning and Graphics, CRC Press, 2015.

Supplemental Texts on Numerical Methods:

David Kincaid and Ward Cheney, Numerical Analysis: Mathematics of Scientific Computing, 3rd Revised Edition, Pure and Applied Undergraduate Texts, American Mathematical Society, 2002.

Richard Burden, Douglas Faires and Annette Burden, Numerical Analysis, 10th Edition, Brooks Cole, 2015.

Joe Hoffman and Steven Frankel, Numerical Methods for Engineers and Scientists, Second Edition, CRC Press, 2001.

Classic Texts on Numerical Methods:

Kendall Atkinson, An Introduction to Numerical Analysis, Second Edition, Wiley, 1989.

Richard Hamming, Numerical Methods for Scientists and Engineers, Second Edition, Dover, 1986.

Eugene Isaacson, Analysis of Numerical Methods, Revised Edition, Dover Books on Mathematics, 1993.

Supplemental Texts on Computer Programming:

JTC1/SC22/WG14, C99 Programming Standard, ISO/IEC, 2007.

Simon Long, Learn to Code with C, MagPi, 2017.

Richard Smedley, Conquer the Command Line, MagPi, 2016.

Classic Texts on Computer Programming:

Brian Kernighan, Dennis Ritchie, C Programming Language, 2nd Edition, Prentice Hall, 1988.

Brian Kernighan, Rob Pike, Unix Programming Environment, Pretice-Hall Software Series, 1984.

Student Learning Outcomes

1. Students will be able to implement a numerical method to solve a nonlinear equation using the bisection method and Newton's method.
2. Students will be able to solve linear systems using direct and iterative methods.
3. Students will be able to construct interpolating functions.

Announcements

[24-Dec-2017] Solutions to Final Part 2

[18-Dec-2017 or 20-Dec-2017] Final Exam

• Answers to Quiz 1.
• Answers to Quiz 2.
• Answers to homework from Chapter 3.
• Answer to Question 3 from Programming Project 2.

• Refer to Section 4.1.4 see also Exercise 4.4 from the text. Given points x_i and y_i in R², write a subroutine to find the matrix A∈R^2×2 and the vector b∈R² which minimizes the sum
  ∑_i || Ax_i+b−y_i ||².

  A subroutine to perform this minimization might appear as

      void findAb(int n,double x[n][2],double y[n][2],
          double A[2][2],double b[2]){
  
          // Fill in code here to solve for A and b.
      }
  

• Refer to Exercise 4.7 from the text. Consider the underdetermined system Ax=b where A∈R^m×n with m<n. Solve the optimization problem
  minimize ||x|| such that Ax=b.

  by taking x=A^T(AA^T)⁻¹b. A subroutine to solve for x might appear as

      void undsolve(int m,int n,double A[m][n],double x[n],double b[m]){
  
          // Fill in code here to solve for x when m<n.
      }
  

• Refer to Exercise 4.8 from the text and also the Wikipedia entry on the Thomas Algorithm. Suppose A∈R^n×n is tridiagonal with the vector v along the diagonal, w on the upper diagonal and u on the lower diagonal. Thus,
  

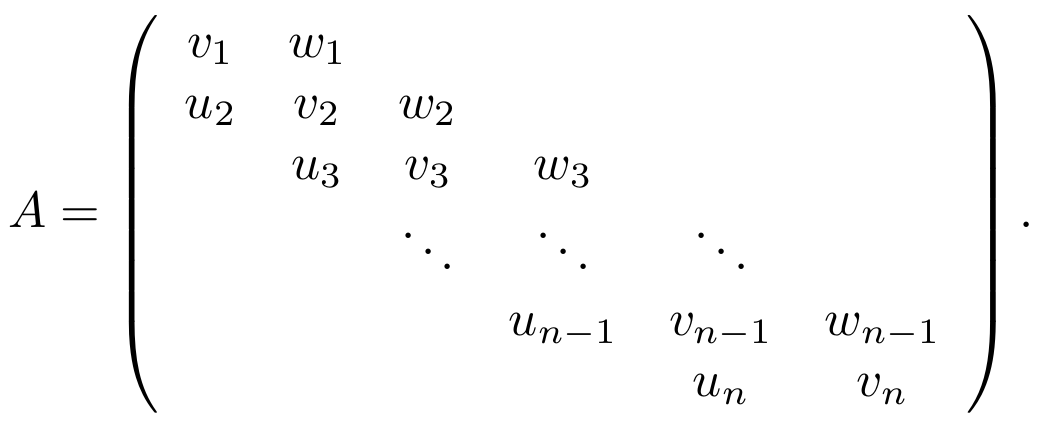
  Assume |u_i|+|w_i|<|v_i| for every i so that Gaussian elimination can be performed without any pivoting to solve Ax=b in order O(n) time. A subroutine to solve for x might appear as

      void tdthomas(int n,double u[n],double v[n],double w[n-1],
  		double x[n],double b[n]){
  
          // Fill in code here to solve for x.
  
          // Note that the first element of the vector u is not
          // used for this computation.
      }
  

[18-Dec-2017 or 20-Dec-2017] Programming Project/Homework 3

[11-Dec-2017] Quiz 2

• State Newton's method for solving f(x)=0.

• Let f be a twice continuously differentiable function and a be a point such that f(a)=0 and f'(a)≠0. Prove that Newton's method is quadratically convergent provided x₀ is close enough to a.

• Explain why it is sometimes said that Newton's method doubles the number of significant digits at each iteration.

[06-Dec-2017] Newton's Method Lecture

[05-Dec-2017] Solutions to Programming Project 2

[30-Nov-2017] Homework Solutions

[27-Nov-2017] In-class Computer Lab

• The video discusses the construction of the DEGIMA supercomputer at Nagasaki University. How much did this supercomputer cost?
• What is a GPU and how many GPUs were used in the construction of the DEGIMA supercomputer?
• The Gordon Bell Prize is an award for outstanding achievments in high-performance computing. The team that assembled the DEGIMA supercomputer won this prize in what year and what category?
• If you had a national grant to make an individualized supercomputer for your own needs, what specialized field or problem would you focus on?

[23-Nov-2017] Solutions to the Midterm

[22-Nov-2017] Midterm Part 2

• Given some data and a linear model perform a linear regression to fit the parameters in the model using a least squares fit.

• Given an invertible matrix find ||A||₂, ||A⁻¹||₂ and cond₂(A).

[21-Nov-2017] Gnuplot

$ gnuplot
gnuplot> f(x)=7.62161-13.8851*x-4.80863*x*x+1.93201*x*x*x
gnuplot> plot "file05a.dat" every ::1 ps 2 pt 5,f(x)

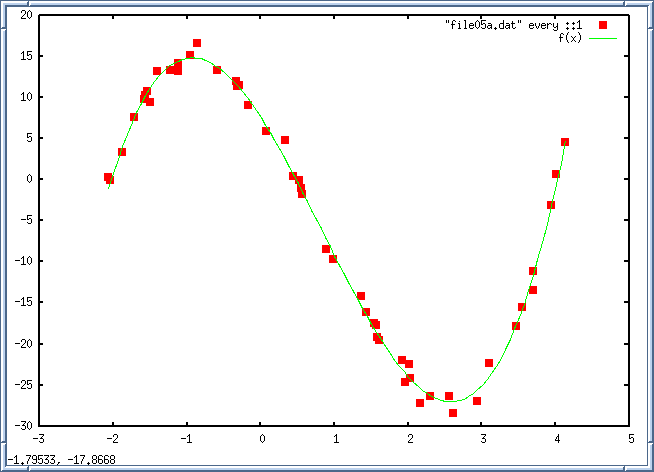
Note that the option every ::1 instructs gnuplot not to plot the first line of the file. We omitted this option in class, but the graph looks better with it included. This is because the first line of the file wasn't data but instead indicated the number of data points in the file.

[20-Nov-2017] Midterm Part 1

• Find the inverse discrete Fourier transform of a vector with length equal to a power of two using a fast conquer-and-divide algorithm.

• Use the PLU factorization to find the inverse matrix.

• Write four subroutines to find the products AB, A^TB, AB^T and A^TB^T of matrices with compatible dimensions.

[15-Nov-2017] Programming Project 2 Due

[13-Nov-2017] Data Files for Linear Regressions

[08-Nov-2017] Video Homework 6 Due

• When Leo Kouwenhoven went to university, what subject was his first choice of study?
• List some possible applications for quantum computing.
• What is a qubit? In theory how much faster is a 32-qubit quantum computer compared to a 16-qubit quantum computer?
• Predict when, if ever, a quantum computer will be available for student use at UNR. Explain your reasoning.

[23-Oct-2017] Video Homework 5 Due

• Who is Jack Dongarra?
• The processors used in the TaihuLight were developed and manufactured in China. How many cores does each processor contain? What is the clock speed of each core?
• How many GFLOPS per watt does TaihuLight achieve?
• Estimate how many GFLOPS per watt are produced by the computers in DMS106. Explain your answer and any assumptions you made.

[18-Oct-2017] Written Homework Due

[11-Oct-2017] Video Homework 4 Due

• What is a sublinear algorithm?
• What is the difference between sample complexity and run-time complexity?
• According to Michael Kapralov, what properties would the ideal Fourier transform algorithm have?
• Do you think such an algorithm exists and will it ever be discovered?

[09-Oct-2017] Quiz 1

[04-Oct-2017] Programming Project 1 Due

[02-Oct-2017] Video Homework 3 Due

• Where is the Citadel Campus located?
• What three energy sources are used to generate the electricity used at the Citadel Campus?
• A Tier 4 datacenter guarantees 99.995% availability. How many minutes could a datacenter be unavailable per year and still meet these requirements?
• What is the advertised network latency from Reno to Las Vegas? How does this compare to the theoretical limits based on the speed of light found in Video Homework 1?

[26-Sep-2017] Fourier Transform Lecture

[25-Sep-2017] Access Files from Windows

[18-Sep-2017] Finding Elapsed Time

[18-Sep-2017] Video Homework 2 Due

[08-Sep-2017] Video Homework 2

• In what country does John Gustafson currently live?
• Show that the dot product of (3.2e8,1,-1,8.0e7) with (4.0e7,1,-1,-1.6e8) is exactly 2.
• What are the advantages of posits compared to floating point numbers?
• Predict when, if ever, hardware that implements posit arithemtic will be available for student use in the UNR computing labs. Explain your reasoning.

[06-Sep-2017] Machine Epsilon

[06-Sep-2017] Video Homework 1 Due

[29-Aug-2017] Video Homework 1

• Who is Grace Hopper?
• How many nanoseconds does it take to travel at the speed of light from Reno to Las Vegas?
• How many picoseconds does each clock cycle of a CPU runing at 2.8 Ghz take?

[12-Aug-2017] Textbook Announced

[10-Jul-2017] Introductory Lecture

[25-Jun-2017] Math/CS 466/666 Linux Image

Extra Credit

1. Write a program to compute the Euler-Mascheroni constant which runs on your cell phone. Report the program, the speed of the program in flops and the type of cell phone used.

2. Consider the programming languages Julia, Maple, Matlab, Kotlin and Go. Determine which languages store matrices in row-major format and which use column-major format.

3. When the real number 0.0 is written to memory using the double precision floating point format, it is stored in 8 bytes as 64 bits all zero. Suppose 0.0 is written to memory using the posit format discussed in Video Lecture 2. Is it true that all the bits in the bytes used to store the number are zero? Explain.

4. Submit a choice of values for a, b and c in Programming Project 1 that is different than the values submitted by any other student.

5. Work problem 3.13abc from the textbook.

6. Define ||x||_p = ( |x₁|^p + |x₂|^p + . . . + |x_n|^p )^1/p and ||x||_∞ = max( |x₁|, |x₂|, . . . , |x_n| ). Prove or disprove the claim that lim_p→∞ ||x||_p = ||x||_∞.

7. The matnorm1 routine written in class computes ||A||₁ by reading the matrix A from memory one column at a time. Write a routine which computes the same norm while reading the matrix row at a time. Compare the speed of your routine with the routine written in class.

8. For n = 10, 20, 40, 80, . . . , 1280 let K_n be the average condition number with respect to the 2-norm of 100 random n × n matrices with entries uniformly distributed between −1 and 1. Plot K_n versus n and try to deduce a relationship between the size of the random matrices and the average condition number.

9. [Midterm Part 2] Let A∈R^n×n be a square invertible matrix. Consider the algorithm
   Repeatedly factorize A=QR and replace A with RQ

   described on page 122 of Numerical Algorithms by Justin Solomon. Write a program that implements this algorithm using one of QR factorization routines written in class. Note that sinze A is square, then R and Q are also square. Under certain conditions the diagonal elements of R will converge to the eigenvalues of A up to a possible sign difference as the program runs. Starting with the matrix contained in the file extra.c print the diagonal elements of R at each iteration to show whether and how they converge.

10. [Computer Lab] Modify your program to find an eigenvector corresponding to the eigenvalue in the top left corner of the eigenvalue plot for the matrix contained in the the matrixA.c file.

11. [Final Exam] Let A and B be matrices such that A^TA=BB^T. Suppose B is invertible and define Q=A(B^T)⁻¹. Prove or disprove the claim that the columns of Q are orthonormal.

Sample Code

• [30-Aug-2017] Euler–Mascheroni Constant (Math)
• [30-Aug-2017] Euler–Mascheroni Constant Serial and Parallel (CS)
• [01-Sep-2017] Euler–Mascheroni Constant Parallel (Math)
• [06-Sep-2017] Machine Epsilon (Math)
• [08-Sep-2017] Machine Epsilon for Long Double (Math)
• [06-Sep-2017] Machine Epsilon (CS)
• [11-Sep-2017] Row or Column Major (Math)
• [11-Sep-2017] Row or Column Major and Matrix Vector Multiplication (CS)
• [13-Sep-2017] Matrix Vector Multiplication (Math)
• [13-Sep-2017] Complex Matrix Vector Multiplication (CS)
• [15-Sep-2017] Refactoring Code and Libraries (Math)
• [18-Sep-2017] Discrete Fourier Transform (Math)
• [18-Sep-2017] Discrete Fourier and Inverse Transform (CS)
• [20-Sep-2017] Inverse Fourier Transform (Math)
• [20-Sep-2017] Fast Fourier Transform (CS)
• [22-Sep-2017] Fast Fourier Transform (Math)
• [25-Sep-2017] Parallel Fast Fourier Transform (Math)
• [25-Sep-2017] Parallel Fast Fourier Transform (CS)
• [29-Sep-2017] LU Factorization (Math)
• [02-Oct-2017] LU Factorization and Backsubstitution (CS)
• [04-Oct-2017] LU Backsubstitution (Math)
• [04-Oct-2017] PLU Factorization (incomplete) (CS)
• [06-Oct-2017] PLU Factorization (Math)
• [09-Oct-2017] PLU Factorization with tictoc (Math)
• [09-Oct-2017] Linpack Benchmark (CS)
• [11-Oct-2017] Linpack Benchmark (Math)
• [11-Oct-2017] AX=B using LAPACKE (CS)
• [13-Oct-2017] AX=B using LAPACKE (Math)
• [16-Oct-2017] Compute ||A||₁ (Math)
• [16-Oct-2017] Compute ||A||₁ (CS)
• [18-Oct-2017] Compute ||A||₂ (incomplete) (CS)
• [23-Oct-2017] Compute ||A||₂ (Math)
• [23-Oct-2017] Compute ||A||₂ (CS)
• [25-Oct-2017] Compute ||A||₂ with stopping condition (Math)
• [25-Oct-2017] Compute ||A||₂ with stopping condition (CS)
• [30-Oct-2017] Gram-Schmidt (incomplete) (Math)
• [30-Oct-2017] Gram-Schmidt (CS)
• [01-Nov-2017] Gram-Schmidt (Math)
• [01-Nov-2017] Householder reflections (incomplete) (CS)
• [03-Nov-2017] Householder reflections (incomplete) (Math)
• [06-Nov-2017] Householder reflections (bad) (Math)
• [06-Nov-2017] Householder reflections (CS)
• [08-Nov-2017] Householder reflections (Math)
• [08-Nov-2017] Householder reflections (CS)
• [13-Nov-2017] Householder reflections (Math)
• [13-Nov-2017] Householder reflections (CS)
• [15-Nov-2017] Least Squares Fit (incomplete) (Math)
• [15-Nov-2017] Least Squares Fit (CS)
• [17-Nov-2017] Least Squares Fit (Math)

Programming Assignments

• Programming Project 1 is due October 4.
• Programming Project 2 is due November 15 (matrices, solution).
• Homework/Programming Project 3 is due at the Final Exam (solution).

Homework Assignments

1. Video Homeworks 1, 2, 3, 4, 5, 6, 7 due as indicated above.
2. Exercises 3.1, 3.6, 3.9, 3.11, 3.15 due October 18 (solutions).

Grading

     2 Quizzes                 20 points each
     1 Exam                    60 points
     1 Final Exam             100 points
     3 Homework Assignments    20 points each
     3 Programming Projects    20 points each
     1 In-class Lab Work       20 points
    ------------------------------------------
                              340 points total

    Grade        Minimum Percentage
      A                 90 %
      B                 80 %
      C                 70 %
      D                 60 %

Final Exam

The final exams are presently scheduled for

• Math Section: Monday, December 18 from 7:30-9:30am in DMS106.
• CS Section: Wednesday, December 20 from 12:10-2:10pm in DMS106.

Equal Opportunity Statement

Academic Conduct