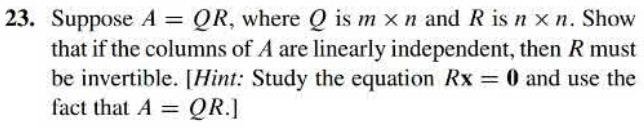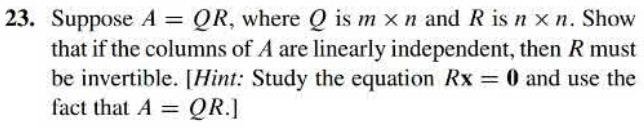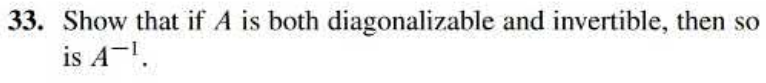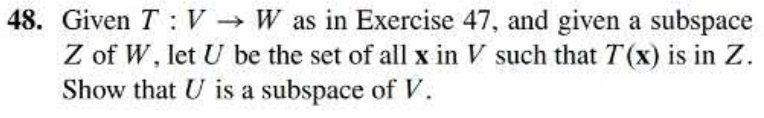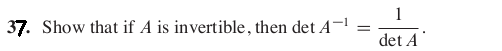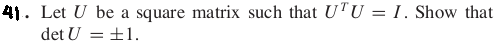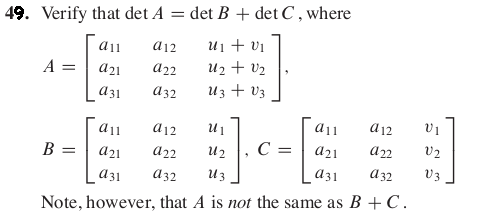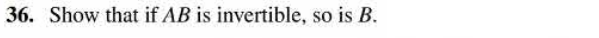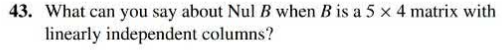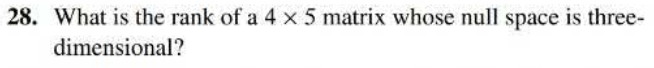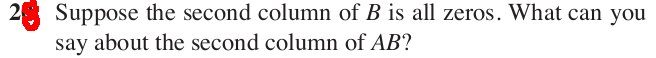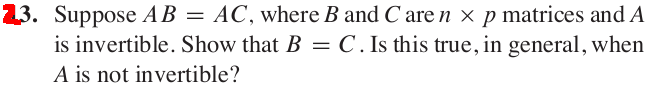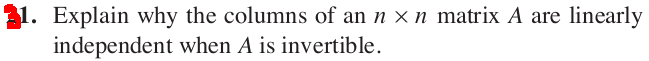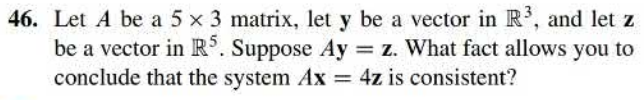Mathematics 330 Homepage

Fall 2023 University of Nevada Reno

330 LINEAR ALGEBRA I (3+0) 3 credits

Vector analysis continued; abstract vector spaces; bases, inner products; projections; orthogonal complements, least squares; linear maps, structure theorems; elementary spectral theory; applications. Corequisite(s): MATH 283 R.

Instructor  Course Section                     Time
------------------------------------------------------------------------
Eric Olson  Math 330-1006 Linear Algebra       11:00-11:50AM MWF PE103

Course Information

Instructor:: Eric Olson
email:: Please contact me through WebCampus
Office:: MWF 1:00-1:50PM in DMS 238 and through Zoom by appointment
Homepage:: http://fractal.math.unr.edu/~ejolson/330/
Live Stream:: If you can't come to class due to sickness, quarantine or other reasons, please join via the Zoom link in WebCampus.
Grader:: to be determined (contact through WebCampus)
Required Texts:: Linear Algebra and Its Applications, n-th Edition by David C. Lay.; https://www.pearson.com/mylab (class registration code)
Other resources:: MIT Open Courseware, Gilbert Strang, Spring 2010.; 18-06-linear-algebra-spring-2010; Introduction to Applied Linear Algebra, Boyd and Vandenberghe.; http://vmls-book.stanford.edu/

Student Learning Outcomes

Upon completion of this course, students will be able to

Solve linear systems using Gaussian elimination.
Minimize least squares by Gram-Schmidt orthogonalization.
Find LU, QR and UΣV^T matrix factorizations.

Lecture Notes

Lecture 1: Overview of the Course
Lecture 2: Systems of Linear Equations
Lecture 3: Unique Solutions
Labor Day: no notes
Lecture 4: Echelon Form
Lecture 5: Solving Systems
Lecture 6: Matrix-Vector Products
Lecture 7: Linear Dependence
Lecture 8: Linear Transformations
Lecture 9: Fish and Sheep
Lecture 10: Matrix-Matrix Products
Lecture 11: Inverse Matrices
Lecture 12: Matrix Transpose
Lecture 13: Matrix of a Row Operation
Lecture 14: LU Factorization
Lecture 15: Col(A) and Nul(A)
Lecture 16: More Subspace Examples
Exam 1: no notes
Lecture 17: Introduction to Determinants
Lecture 18: Determinants and Row Operations
Lecture 19: Determinants and Invertibility
Lecture 20: Cramer's Rule
Lecture 21: Formula for the Inverse
Lecture 22: Subspaces Again
Lecture 23: More Subspaces
Lecture 24: Even More Subspaces
Nevada Day: no notes
Lecture 25: The Basis Theorem
Lecture 26: Change of Basis
Lecture 27: Eigenvalues and Eigenvectors
Lecture 28: Characteristic Polynomial
Lecture 29: Diagonalization
Veteran's Day: no notes
Lecture 30: Basis of a Linear Transformation
Lecture 31: Complex Numbers
Exam 2: no notes
Lecture 32: Complex Eigenvalues
Lecture 33: Orthogonality
Thanksgiving: no notes
Lecture 34: Orthogonal Projections
Lecture 35: Gram-Schmidt
Lecture 36: QR and Least Squares
Lecture 37: QR Factorization Example
Lecture 38: The Spectral Theorem
Lecture 39: Singular Value Decomposition
Review: Final Exam Review

Solutions to Written Homework

Announcements

[20-Dec-2023] Final Exam

The final exam will be Wednesday, December 20, 2023 from 10:15am-12:15pm in PE103. Here are two sample final exams for review.

A review session has been scheduled at the UNR Mathematics Center on December 17 from 3:30 to 5:30pm to discuss these sample exams and any other questions you may have.

[11-Dec-2023] Written Homework 7 Solutions

I've made solutions for written homework 7 to help you study. Please let me know if you have questions or see any errors.

[06-Dec-2023] Written Homework 7

Written Homework 7 is due December 6 consisting of the following questions:

Section 6.1 # 35
Section 6.4 # 23
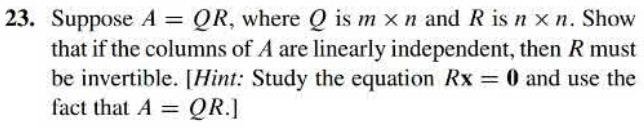
Section 6.4 # 24

[29-Nov-2023] Written Homework 6 Solutions

I've made solutions for written homework 6 to help you study. Please let me know if you have questions or see any errors.

[17-Nov-2023] Exam 2

The second in-class exam will be November 17 and cover up to and including Section 5.4. Here are two sample exams to help you review for the exam.

[16-Nov-2023] Review for Exam 2

The Math Center has scheduled a review session for our section of Math 330 on Thursday, November 16th from 4:30-6pm in the Math Center (PSAC 300).

[15-Nov-2023] Written Homework 6

Written Homework 6 is due November 15 consisting of the following questions:

Section 5.1 # 31
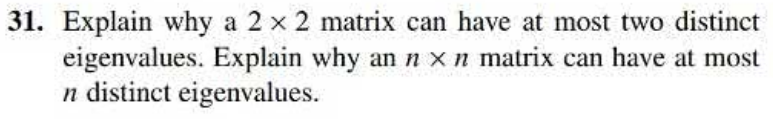
Section 5.2 # 20
Section 5.3 # 33

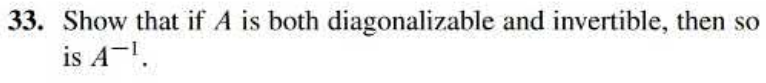
[12-Nov-2023] Written Homework 5 Solutions

I've made solutions for written homework 5 to help you study. Please let me know if you have questions or see any errors.

[03-Nov-2023] Written Homework 5

Written Homework 5 is due November 3 consisting of the following questions:

Section 4.1 # 40
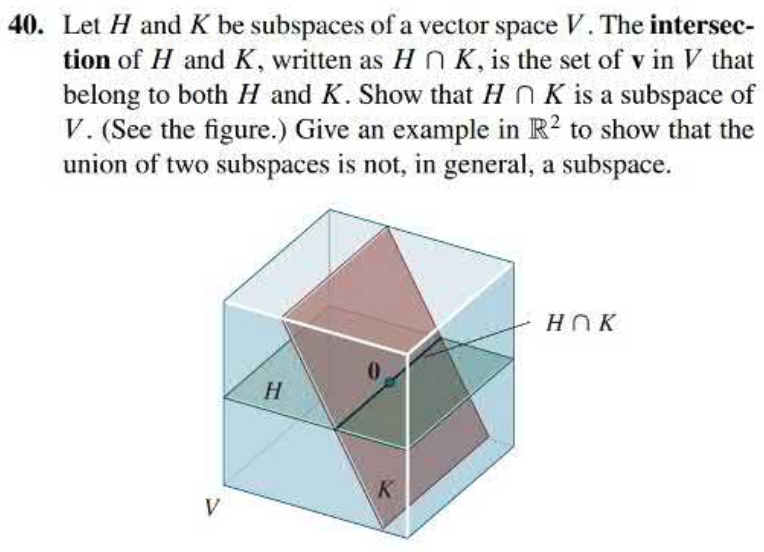
Section 4.2 # 47
Section 4.2 # 48

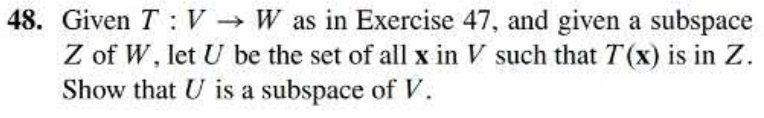
[27-Oct-2023] Written Homework 4 Solutions

I've made solutions for written homework 4 to help you study. Please let me know if you have questions or see any errors.

[20-Oct-2023] Written Homework 4

Written Homework 4 is due October 20 consisting of the following questions:

Section 3.2 # 37
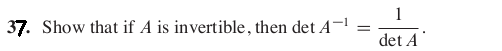
Section 3.2 # 41
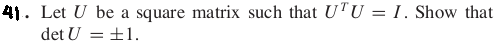
Section 3.2 # 49

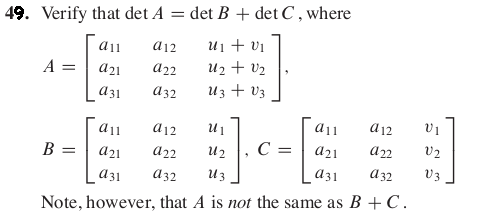
[16-Oct-2023] Written Homework 3 Solutions

I've made solutions for written homework 3 to help you study. Please let me know if you have questions or see any errors.

[13-Oct-2023] Written Homework 3

Written Homework 3 is due October 13 consisting of the following questions:

Section 2.3 # 36
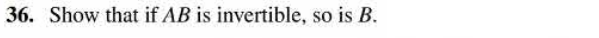
Section 2.8 # 43
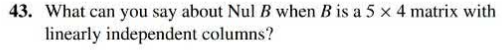
Section 2.9 # 28

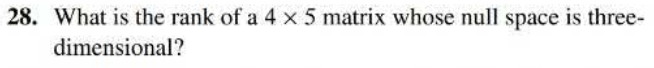
[6-Oct-2023] Exam 1

The first in-class exam will be October 6 and cover up to and including Section 2.5. Here are two sample exams to help you review for the exam.

[5-Oct-2023] Review for Exam 1

I will hold a review session for Exam 1 on October 5 at 1pm through Zoom at the usual meeting number available on WebCampus. A recording of the review session is now available on WebCampus. Click the Zoom link at the left and then click on Cloud Recordings tab.

[1-Oct-2023] Written Homework 2 Solutions

I've made solutions for written homework 2 to help you study. Please let me know if you have questions or see any errors.

[29-Sep-2023] Written Homework 2

Written Homework 2 is due September 29 consisting of the following questions:

Section 2.1 # 28
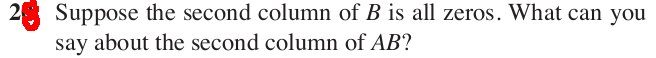
Section 2.2 # 23
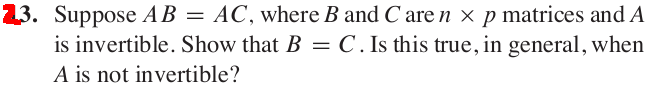
Section 2.2 # 31

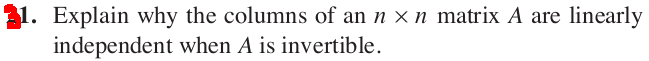
[24-Sep-2023] Written Homework 1 Solutions

I've made solutions for written homework 1 to help you study. Please let me know if you have questions or see any errors.

[15-Sep-2023] Written Homework 1

Written Homework 1 is due September 15 consisting of the following questions:

Section 1.4 # 14
Section 1.4 # 44
Section 1.4 # 46

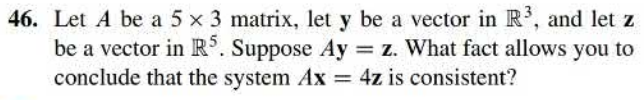
[01-Sep-2023] MyLab Updated

I have updated the online homework on the Pearson website for this course. Please let me know if anything looks wrong or you have trouble accessing the homework.

[28-Aug-2023] Peason Math MyLab

Registration infomation for this section of Pearson Mylab is now available. It is recommended you choose "Get temporary access without payment for 14 days" as the university will not be able to refund the money you pay to Pearson if you drop the course in the first weeks of class.

[27-Aug-2023] Welcome Fall 2023

I am looking forward to seeing you August 28 starting the first week of class. We will also live stream our class meetings at a link available in WebCampus and maintain an online archive of course materials including lecture notes, assignments and other announcements. The live stream is so people unable to attend on a particular day can stay informed and have an easier time to catch up. To promote a learning environment where people feel free to ask questions, no recordings will be made. Please do not view the live stream from the classroom as that can cause network lag and audio feedback.

My lecture notes should complement the notes you take in class. I'd recommend comparing the notes you take with the ones I post after class along with the relevant sections from the text. Then use these three sources of information to create a final version of your notes. In my experience reviewing the lecture in this way is important. Though tempting with an iPad, one should not try make the final version of your lecture notes during class. That takes too much time and omits the comparison and review steps mentioned above.

We will be using WebCampus to turn in written homework--either scanned from pencil and paper or prepared digitally using an iPad or similar device. In addition there will be online exercises available from the Pearson MyLab webpage. In addition to the exercises and written homework, there will be two exams and a final exam. In person attendance is mandatory for all exams and the final.

Grading

     Exam 1                    50 points
     Exam 2                    50 points
     MyLab Math Online         50 points
     Handwritten Homework      50 points
     Final                    100 points
    ------------------------------------------
                              300 points total

Exams and quizzes will be interpreted according to the following grading scale:

    Grade        Minimum Percentage
      A                 90 %
      B                 80 %
      C                 70 %
      D                 60 %

The instructor reserves the right to give plus or minus grades and higher grades than shown on the scale if it is believed they are warranted.

Quiz and Exam Schedule

There will be two exams each one covers material from the start of the course up to the time the exam is given. The final exam will be cumulative and test everything learned the entire semester. Details and a study guide will be provided prior to each exam. In person attendance is mandatory for all exams and the final.

Aug 28 -- Overview of the Text
Aug 30 -- Section 1.1 Systems of Linear Equations
Sep 01 -- Section 1.2 Row Reduction and Echelon Forms

Sep 04 ***Labor Day***
Sep 06 -- Section 1.4 The Matrix Equations Ax=b
Sep 08 -- Section 1.5 Solution Sets of Linear Systems

Sep 11 -- Section 1.5 Solution Sets of Linear Systems (continued)
Sep 13 -- Section 1.7 Linear Independence
Sep 15 -- Section 1.8 Introduction to Linear Transforms
          Section 1.9 The Matrix of a Linear Transformation

Sep 18 -- Section 2.1 Matrix Operations
Sep 20 -- Section 2.2 The Inverse of a Matrix
Sep 21 -- Section 2.3 Characterizations of Invertible Matrices

Sep 25 -- Section 2.4 Partitioned Matrices
Sep 27 -- Section 2.5 Matrix Factorizations
Sep 29 -- Section 2.5 Matrix Factorizations (continued)

Oct 02 -- Section 2.8 Subspaces of Rⁿ
Oct 04 -- Section 2.9 Dimension and Rank
Oct 06 -- Exam 1

Oct 09 -- Section 3.1 Introduction to Determinants
Oct 11 -- Section 3.2 Properties of Determinants
Oct 13 -- Section 3.3 Cramer's Rule, Volume and Linear
          Transformations

Oct 16 -- Section 3.3 Cramer's Rule, Volume and Linear 
          Transformations (continued)
Oct 18 -- Section 4.1 Vector Spaces and Subspaces
Oct 20 -- Section 4.2 Null Spaces, Column Spaces, Row Spaces
          and Linear Transformations

Oct 23 -- Section 4.2 Null Spaces, Column Spaces, Row Spaces
          and Linear Transformations (continued)
Oct 25 -- Section 4.3 Linearly Independent Sets; Bases
Oct 27 ***Nevada Day***

Oct 30 -- Section 4.5 The Dimension of a Subspace
Nov 01 -- Section 4.6 Change of Basis
Nov 03 -- Section 5.1 Eigenvalues and Eigenvectors

Nov 06 -- Section 5.2 The Characteristic Equations
Nov 08 -- Section 5.3 Diagonalization
Nov 10 ***Veteran's Day***

Nov 13 -- Section 5.4 Eigenvectors and Linear Transformations
Nov 15 -- Section 5.5 Complex Eigenvalues
Nov 17 -- Exam 2

Nov 20 -- Section 6.1 Inner Product, Length and Orthogonality
Nov 22 -- Section 6.2 Orthogonal Sets
Nov 24 ***Family Day***

Nov 27 -- Section 6.3 Orthogonal Projections
Nov 29 -- Section 6.4 The Gram-Schmidt Process
Dec 01 -- Section 6.5 Least Squares Problems

Dec 04 -- Section 7.1 Diagonalization of Symmetric Matrices
Dec 06 -- Section 7.4 The Singular Value Decomposition
Dec 08 -- Section 7.4 The Singular Value Decomposition (continued)

Dec 11 -- Review
Dec 13 ***Prep Day***

Dec 20 Final Exam from 10:15am-12:15pm

Course Policies

Communications Policy

Lectures and classroom activities will held in person and live streamed through through Zoom at the scheduled meeting time listed in MyNevada for this course. Please check the canvas page for the Meeting ID and Join URL under the Zoom tab if you are unable to make it to class.

During the epidemic I discovered that Zoom also allowed me to meet individually with students who are sick or can't come to campus just to ask a question. If you wish to set up an appointment for office hours please send me a message through WebCampus.

Late Policy

Students must have an approved university excuse to be eligible for a make-up exam. If you know that you will miss a scheduled exam please let me know as soon as possible.

Plagiarism

Students are encouraged to work in groups and consult resources outside of the required textbook when doing the homework for this class. Please cite any sources you used to complete your work including Wikipedia, other books, online discussion groups, generative AI such as ChatGPT as well as personal communications. Note that answers obtained from any source should be verified and fully understood for homework to have a positive learning outcome. In all cases your sources need to be cited.

Exams and quizzes, unless otherwise noted, will be closed book, closed notes and must reflect your own independent work.

Academic Conduct

Bring your student identification to all exams. Work independently on all exams and quizzes. Behaviors inappropriate to test taking may disturb other students and will be considered cheating. Don't send electronic messages, talk or pass notes with other students during a quiz or exam. Homework may be discussed freely. When taking a quiz or exam don't read notes or books unless explicitly permitted. Sanctions for violations are specified in the University Academic Standards Policy.

If you are unclear as to what constitutes cheating, please consult with me.

Statement on Academic Success Services

Your student fees cover usage of the University Math Center, University Tutoring Center, and University Writing and Speaking Center. These centers support your classroom learning; it is your responsibility to take advantage of their services. Keep in mind that seeking help outside of class is the sign of a responsible and successful student.

Equal Opportunity Statement

The University of Nevada Department of Mathematics and Statistics is committed to equal opportunity in education for all students, including those with documented physical disabilities or documented learning disabilities. University policy states that it is the responsibility of students with documented disabilities to speak with the Disability Resource Center during the first week of each semester to discuss appropriate accommodations to ensure equity in grading, classroom experiences and outside assignments. For assistance with accessibility, or to report an issue, please use the Accessibility Help Form. The form is set up to automatically route your request to the appropriate office that can best assist you.

Diversity

This course is designed to comply with UNR Core Objective 10. More information about the core curriculum may be found in the UNR Catalog here.

Statement on Audio and Video Recording

Surreptitious or covert video-taping of class or unauthorized audio recording of class is prohibited by law and by Board of Regents policy. This class may be videotaped or audio recorded only with the written permission of the instructor. In order to accommodate students with disabilities, some students may be given permission to record class lectures and discussions. Therefore, students should understand that their comments during class may be recorded.

Final Exam

The final exams will be held in person at the time listed in the standard schedule of final exams for this section. Namely, the final exam is Wednesday, December 20, 2023 from 10:15am-12:15pm in PE103.

Last Updated: Sat Aug 26 10:48:12 AM PDT 2023